利用MATLAB对三自由度机械臂系统进行仿真

本篇文章主要讲述利用MATLAB Simulink中的Simscape Multibody（SimMechanics）模块对三自由度机械臂系统进行仿真。适用于同济大学机械原理课程设计课程（至少我那阵是做这个）。

📓题目

在 MATLAB / Multibody 环境中，实现 3 自由度机械臂运动仿真。

具体要求：

机械臂的 3 个关节均为转动副。基础坐标系的方向如下图所示，但基础坐标系的原点位置可以任意选定。初始时刻第 1 个转动副的轴线沿基础坐标系 z 轴，第 2、3 个转动副轴线均沿基础坐标系 x 轴。

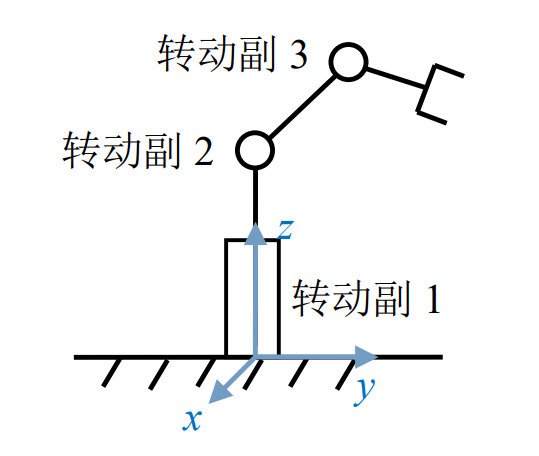
机械臂的杆件结构参数（包括杆件长度）自由设计；所建立的 Multibody 模型（可以在 Multibody 建模，也可以利用其它三维设计软件的 step 格式）要求包含机械臂关节和末端执行器的细节结构。
机械臂在初始时刻的位置姿态自行确定；经过 5 秒，机械臂末端执行器沿直线运动到目标点：x=0.5m，y=0.6m，z=1.3m；5 秒之后，机械臂停留在目标点。

1️⃣机械臂仿真内容介绍

本题要求为：机械臂在初始时刻姿态自行确定；经过5s机械臂末端执行器沿直线运动到目标点x=0.5m、y=0.6m、z=1.3m，5s之后，机械臂停留在目标点。

为实现上述要求，相关解决方式及主要模块功能如下：

利用SolidWorks建立机械臂模型，并导出step格式，用File Solid模块导入到MATLAB中，其中，主要杆件的相关结构参数如下：

表1 Multibody（SimMechanics）模型杆件相关结构参数

参数	数值
转动副2回转中心到转动副1的距离L1	0.3m
转动副2、3之间的距离L2	0.7m
转动副3回转中心到夹持端夹持中心的距离L3	0.7m

利用坐标变换（Rigid Transform）模块调整各杆件位置，机械臂初始位置为x=0，y=1.4m，z=0.3m；修改各转动副（Revolute Joint）模块参数，添加信号输入、输出端口，并连接PID模块以实现位置控制。
根据位置方程计算得位置反解函数，利用MATLAB Function模块编写运动学反解程序；利用Fcn模块、Clock时钟模块和Switch模块输入x，y，z与时钟变量u的关系，并实现运动状态的切换。
调试PID参数，以获得更加平稳、更接近直线轨迹的运动。

2️⃣机械臂仿真相关图片

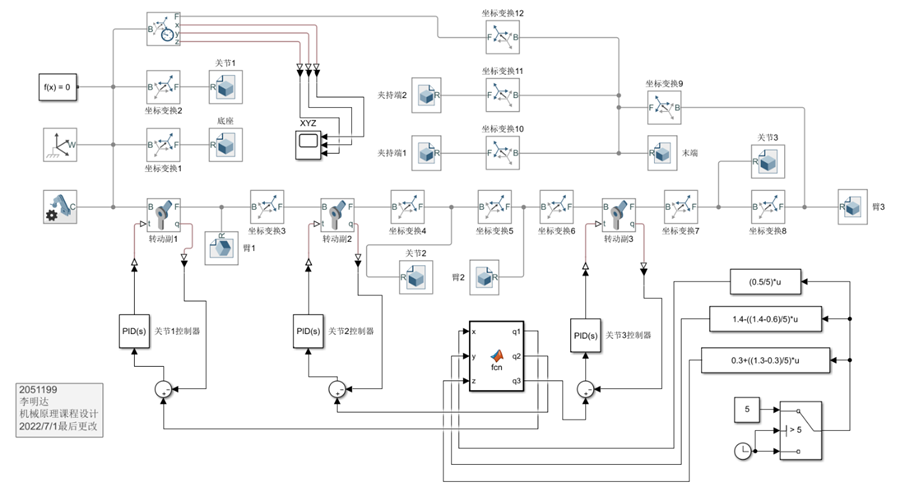
图1 Multibody（SimMechanics）模型图

图2 机械臂初始时刻截图

图3 机械臂运动过程中截图

图4 机械臂到达目标点截图

3️⃣MATLAB程序片段

3.1 机械臂位置反解

%% 机械臂位置反解程序
syms L1 L2 L3 q1 q2 q3 x y u
eqn2 = L2*cos(q2)+L3*cos(q2+q3) == sqrt(x^2+y^2);   %利用x^2+y^2与q2,q3的关系式，简化运算
eqn3 = L2*sin(q2)+L3*sin(q2+q3) == u;               %此处u = z-L1
[q2 ,q3] = solve(eqn2, eqn3 ,q2, q3)

3.2 Multibody中机械臂位置反解模块

function [q1,q2,q3] = fcn(x,y,z)
%% 函数说明
% In: 目标点坐标x,y,z;
% Out: 各关节转角q1,q2,q3;
%% 结构参数
L1 = 0.3;    % 转动副2回转中心到转动副1的距离
L2 = 0.7;    % 转动副2、3之间的距离
L3 = 0.7;    % 转动副3回转中心到夹持端夹持中心的距离 
%% 运动学逆解
u  = z-L1;
q1 = -atan2(x,y);   %q1可以利用x和y来直接表示，从而简化方程
q2 = 2*atan((2*L2*u - (L2^2*((L2^2 + 2*L2*L3 + L3^2 - u^2 - x^2 - y^2)*(- L2^2 + 2*L2*L3 - L3^2 + u^2 + x^2 + y^2))^(1/2))/(- L2^2 + 2*L2*L3 - L3^2 + u^2 + x^2 + y^2) - (L3^2*((L2^2 + 2*L2*L3 + L3^2 - u^2 - x^2 - y^2)*(- L2^2 + 2*L2*L3 - L3^2 + u^2 + x^2 + y^2))^(1/2))/(- L2^2 + 2*L2*L3 - L3^2 + u^2 + x^2 + y^2) + (u^2*((L2^2 + 2*L2*L3 + L3^2 - u^2 - x^2 - y^2)*(- L2^2 + 2*L2*L3 - L3^2 + u^2 + x^2 + y^2))^(1/2))/(- L2^2 + 2*L2*L3 - L3^2 + u^2 + x^2 + y^2) + ((x^2 + y^2)*((L2^2 + 2*L2*L3 + L3^2 - u^2 - x^2 - y^2)*(- L2^2 + 2*L2*L3 - L3^2 + u^2 + x^2 + y^2))^(1/2))/(- L2^2 + 2*L2*L3 - L3^2 + u^2 + x^2 + y^2) + (2*L2*L3*((L2^2 + 2*L2*L3 + L3^2 - u^2 - x^2 - y^2)*(- L2^2 + 2*L2*L3 - L3^2 + u^2 + x^2 + y^2))^(1/2))/(- L2^2 + 2*L2*L3 - L3^2 + u^2 + x^2 + y^2))/(2*L2*(x^2 + y^2)^(1/2) + L2^2 - L3^2 + u^2 + x^2 + y^2));
q3 = -2*atan(((L2^2 + 2*L2*L3 + L3^2 - u^2 - x^2 - y^2)*(- L2^2 + 2*L2*L3 - L3^2 + u^2 + x^2 + y^2))^(1/2)/(- L2^2 + 2*L2*L3 - L3^2 + u^2 + x^2 + y^2));
end

如需相关资料，烦请邮箱联系。